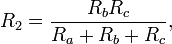Star to delta Transformation And Vice Versa

 The Y-Δ transform, also written Y-delta, Wye-delta, Kennelly’s delta-star transformation, star-mesh transformation, T-Π or T-pi transform, is a mathematical technique to simplify the analysis of an electrical network.

Equations for the transformation from Δ-load to Y-load 3-phase circuit

The general idea is to compute the impedance R_y at a terminal node of the Y circuit with impedances R', R'' to adjacent nodes in the Δ circuit by

where R_Δ are all impedances in the Δ circuit. This yields the specific formulae

Equations for the transformation from Y-load to Δ-load 3-phase circuit

The general idea is to compute an impedance R_Δ in the Δ circuit by

where R_P = R₁R₂ + R₂R₃ + R₃R₁ is the sum of the products of all pairs of impedances in the Y circuit and R_opposite is the impedance of the node in the Y circuit which is opposite the edge with R_Δ. The formula for the individual edges are thus

Graph theory

In graph theory, the Y-Δ transform means replacing a Y subgraph of a graph with the equivalent Δ subgraph. The transform preserves the number of edges in a graph, but not the number of vertices or the number of cycles. Two graphs are said to be Y-Δ equivalent if one can be obtained from the other by a series of Y-Δ transforms in either direction. For example, the Petersen graph family is a Y-Δ equivalence class.

Demonstration

Δ-load to Y-load transformation equations

Δ and Y circuits with the labels that are used in this article.

To relate {R_a,R_b,R_c} from Δ to {R₁,R₂,R₃} from Y, the impedance between two corresponding nodes is compared. The impedance in either configuration is determined as if one of the nodes is disconnected from the circuit.
The impedance between N₁ and N₂ with N₃ disconnected in Δ:

To simplify, let's call R_T the sum of {R_a,R_b,R_c}.

R_T = R_a + R_b + R_c

Thus,

The corresponding impedance between N₁ and N₂ in Y is simple:

R_Y(N₁,N₂) = R₁ + R₂

hence:

  (1)

Repeating for R(N₂,N₃):

  (2)

and for R(N₁,N₃):

  (3)

From here, the values of {R₁,R₂,R₃} can be determined by linear combination (addition and/or subtraction).
For example, adding (1) and (3), then subtracting (2) yields

thus,

where R_T = R_a + R_b + R_c
For completeness:

(4)

(5)

(6)

[edit] Y-load to Δ-load transformation equations

Let

R_T = R_a + R_b + R_c.

We can write the Δ to Y equations as

  (1)

  (2)

  (3)

Multiplying the pairs of equations yields

  (4)

  (5)

  (6)

and the sum of these equations is

  (7)

Factor R_aR_bR_c from the right side, leaving R_T in the numerator, canceling with an R_T in the denominator.

(8)

-Note the similarity between (8) and {(1),(2),(3)}
Divide (8) by (1)

which is the equation for R_c. Dividing (8) by R₂ or R₃ gives the other equations.